티스토리 뷰
2. 알고리즘 분석
알고리즘 분석의 가장 중요한 도구는 1) RAM 계산 모델 2) 최악의 경우(worst-case)의 점근적 분석(asymptotic analysis)이다.
RAM 계산 모델
기계-독립적인 알고리즘 설계는 임의 접근 기계(Random Access Machine: RAM) 가상의 컴퓨터에 달려있다.
가상의 컴퓨터의 특징
- 각각의 단순 연산은 하나의 단계 동안에 실행
- 루프와 서브루틴은 단순 연산이 아니다.
- 메모리 접근은 하나의 단계 동안에 이루어진다. 메모리 크기는 무한하여, 원하는 만큼의 메모리를 사용할 수 있다.
알고리즘을 언어와 기계에 독립적인 방식으로 이해하고 연구할 수 있다.
최선, 최악, 평균의 경우 복잡도
RAM 계산 모델을 사용하면 알고리즘이 몇 개의 단계를 실행하는지 헤아릴 수 있다.
모든 입력 사례에 대하여 동작하는 것을 보고 좋은 알고리즘인지 판별할 수 있다.

x-축은 입력 문제의 크기, y-축은 각 사례에 대한 알고리즘이 실행한 단계의 계수
- 최악의 경우(worst-case) : 크기 n인 모든 사례에 대한 단계의 최대 개수 --> 실제에서 가장 유용
- 최선의 경우(best-case) : 크기 n인 모든 사례에 대한 단계의 최소 개수
- 평균의 경우(average-case) : 크기 n인 모든 사례에 대한 단계의 평균 개수
시간 복잡도(time complexitiy) 각각은 문제 크기에 따른 시간을 수치 함수로 정의 ex) y^3 = x^2 - 2x + 1
대문자 O 표기를 사용하여 시간 복잡도 함수의 상계(upper bound)와 하계(lower bound)를 구할 수 있으며 세부 사항을 무시하여 분석을 훨씬 단순화한다.
ex) f(n) = 2n 과 g(n) = n은 대문자 O 분석에서는 같은 것
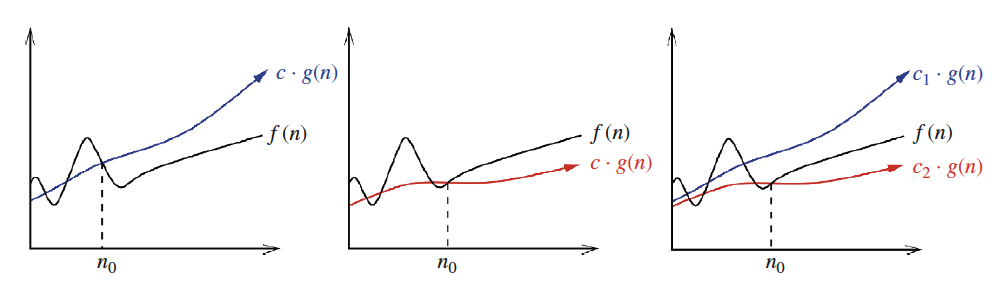
- f(n) = O(g(n))은 c*g(n)이 f(n)의 상계(upper bound)임을 의미, f(n) <= c * g(n)
- f(n) = Ω(g(n))은 c*g(n)이 f(n)의 하계(lower bound)임을 의미, f(n) >= c * g(n)
- f(n) = Θ(g(n))은 c1 * g(n)은 f(n)의 상계, c2 * g(n)은 f(n)의 하계, c2* g(n) <= f(n) <= c1 * g(n), 엄격한 한계(tight bound)
대문자 O 표기와 최악의 경우 분석은 알고리즘의 효율성을 비교하는 작업을 매우 단순화해주는 도구
알고리즘이 자세히 설계되어 있으면 알고리즘의 실행 시간에 대한 추론이 쉽다.
선택 정렬(Selection Sort)
selection_sort(int s[], int n) {
int i, j;
int min;
for (i = 0; i < n; i++) {
min = i;
for (int j = i + 1; j< n; j++)
if (s[j] < s[min]) min = j;
swap(&s[i], &s[min]);
}
}바깥 루프(loop)는 n번, 안쪽 루프는 n - i - 1번 돌아간다.

T(n) = (n - 1) + (n - 2) + (n - 3) + .... + 2 + 1
T(n) ≈ (n - 1)n/2 = O(n^2), 제곱 시간 알고리즘
삽입 정렬(Selection Sort)
for (i = 1; i < n; i++) {
j = i;
while ((j > 0) && (s[j] < s[j - 1])) {
swap(&s[j], &s[j - 1]);
j = j - 1;
}
}바깥 루프는 n번, 안쪽 루프는 항상 i회 반복 가정 i < n이므로 항상 n회 반복
O(n^2) 제곱 시간 알고리즘
로그와 이진 탐색
이진 탐색(binary search)는 O(logn) 알고리즘의 좋은 예
ex) 가나다순 전화번호부에서 특정한 사람 p를 찾기 위해 한가운데 n / 2번째 이름과 비교, 한 번 비교한 이후에 전화번호부에 있는 이름 절반 고려하여 제외 가능, 오직 하나가 남을 때까지 반으로 나누는 횟수와 같다 (log2n)
로그와 트리
높이(height)가 1인 이진 트리는 최대 2개까지 리프(leaf)를 가질 수 있다. 높이가 2이면 4개의 리프 노드
n개는 n = 2^h, h = log2n을 의미한다.
로그는 무엇이든 반복하여 반으로 줄어들거나 두 배가 될 때 나타난다.
'Computer Science > Algorithm' 카테고리의 다른 글
| 그래프 순회(Graph Traversal) - 1 (0) | 2021.04.15 |
|---|---|
| 정렬과 탐색(Sort & Search) - 2 (0) | 2021.04.13 |
| 정렬과 탐색(Sort & Search) - 1 (0) | 2021.04.12 |
| 자료 구조(Data Structures) - 2 (0) | 2021.04.11 |
| 자료 구조(Data Structures) - 1 (0) | 2021.04.08 |
